Exponents are a fundamental concept in mathematics that represent repeated multiplication. Understanding the division properties of exponents is crucial for simplifying expressions and solving equations. Let’s dive into this topic and uncover some helpful tips!
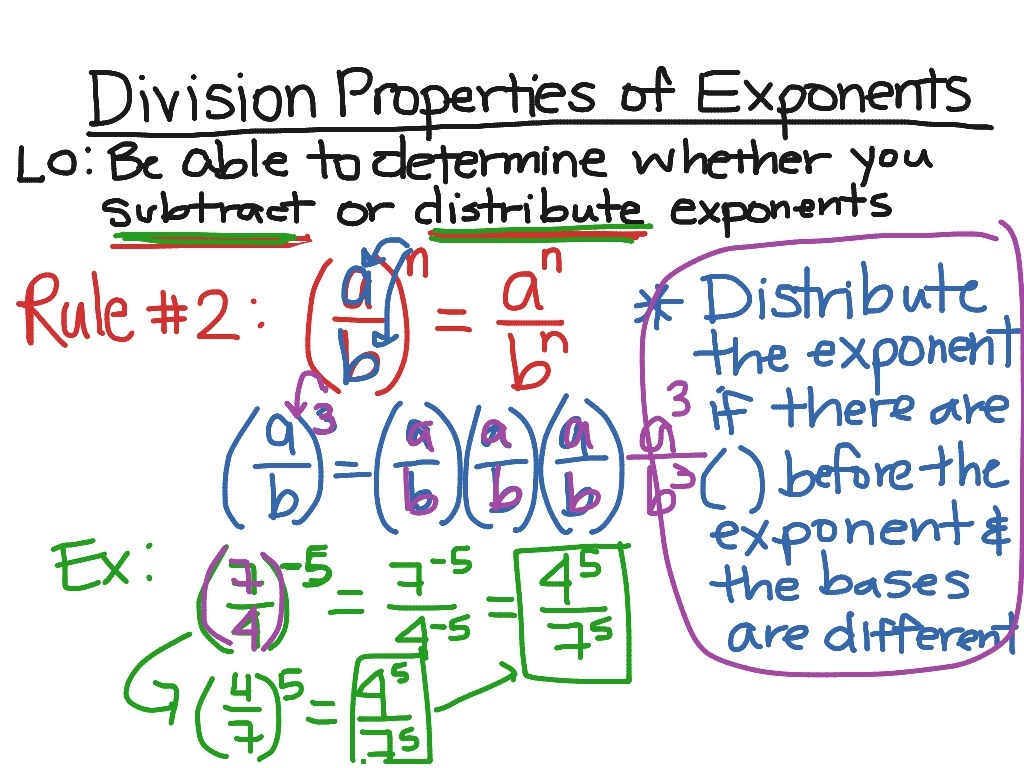
When dividing terms with the same base but different exponents, you can simply subtract the exponents to simplify the expression. For example, when dividing x^5 by x^2, you subtract 2 from 5 to get x^3. This rule applies to all bases, not just x.

division properties of exponents
Exploring the Division Properties of Exponents
Another important rule is that any number raised to the power of zero is equal to 1. This means that x^0 = 1, y^0 = 1, and so on. It is a fundamental property of exponents that helps simplify calculations and equations.
When dividing terms with different bases but the same exponent, you can treat each base separately and simplify the expression accordingly. For instance, when dividing 2^3 by 4^3, you simplify it as (2/4)^3 = (1/2)^3 = 1/8.
Remember that the division properties of exponents apply to both positive and negative exponents. When dividing terms with negative exponents, you can move them to the denominator by changing the sign of the exponent. This helps simplify the expression and make calculations easier.
In conclusion, mastering the division properties of exponents is essential for solving complex mathematical problems efficiently. By understanding these rules and practicing them regularly, you can streamline your calculations and tackle challenging equations with confidence. Keep exploring and applying these principles to enhance your mathematical skills!
Division Properties Of Exponents Math ShowMe
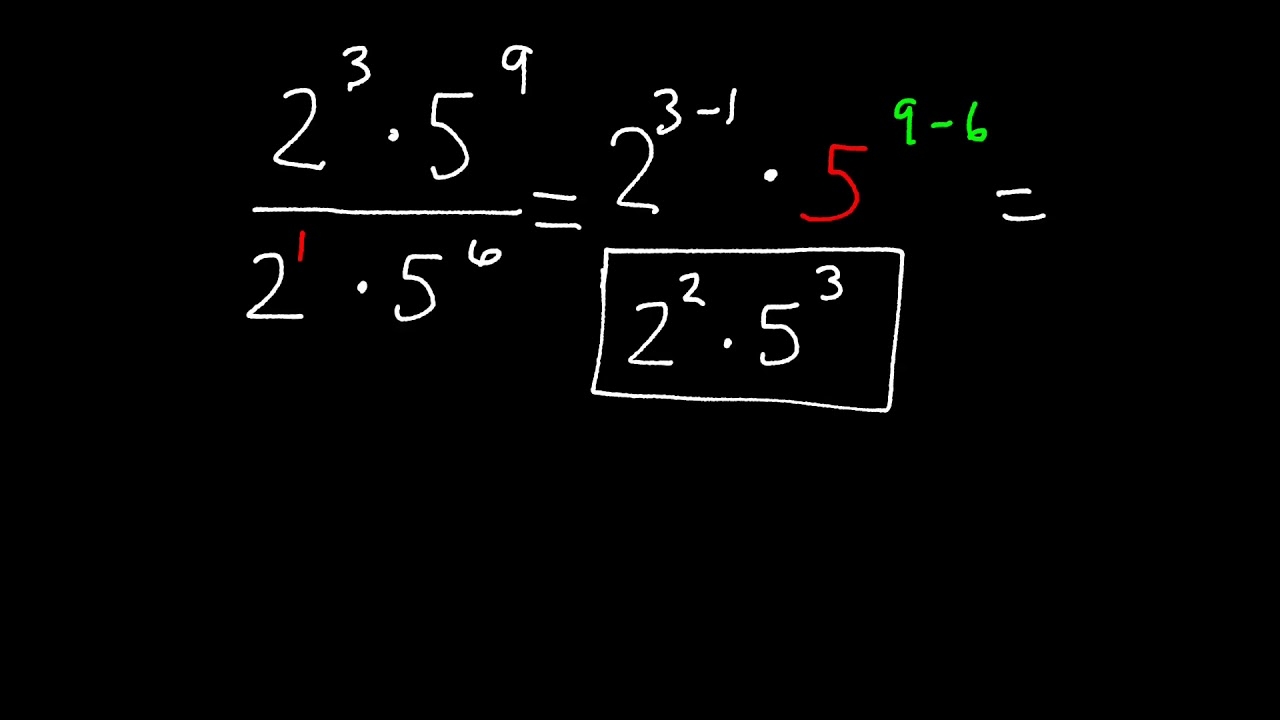
Division Properties Of Exponents YouTube
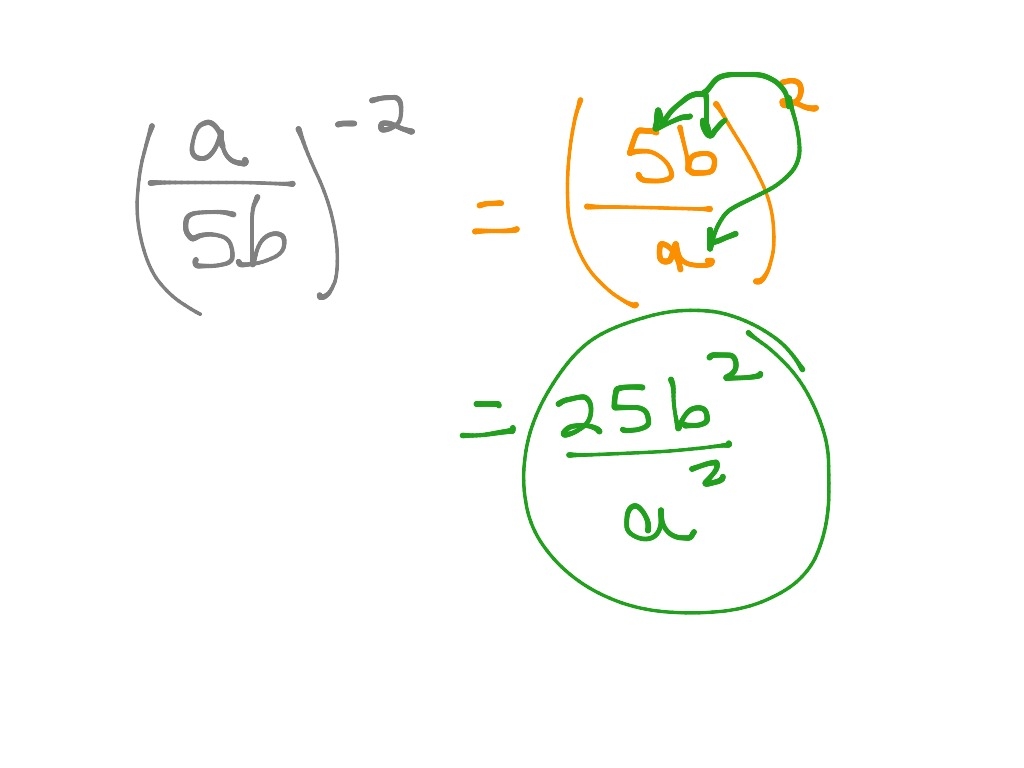
Division Properties Of Exponents Math Algebra Exponents ShowMe

Division Properties Of Exponents YouTube

Division Properties Of Exponents 1 YouTube