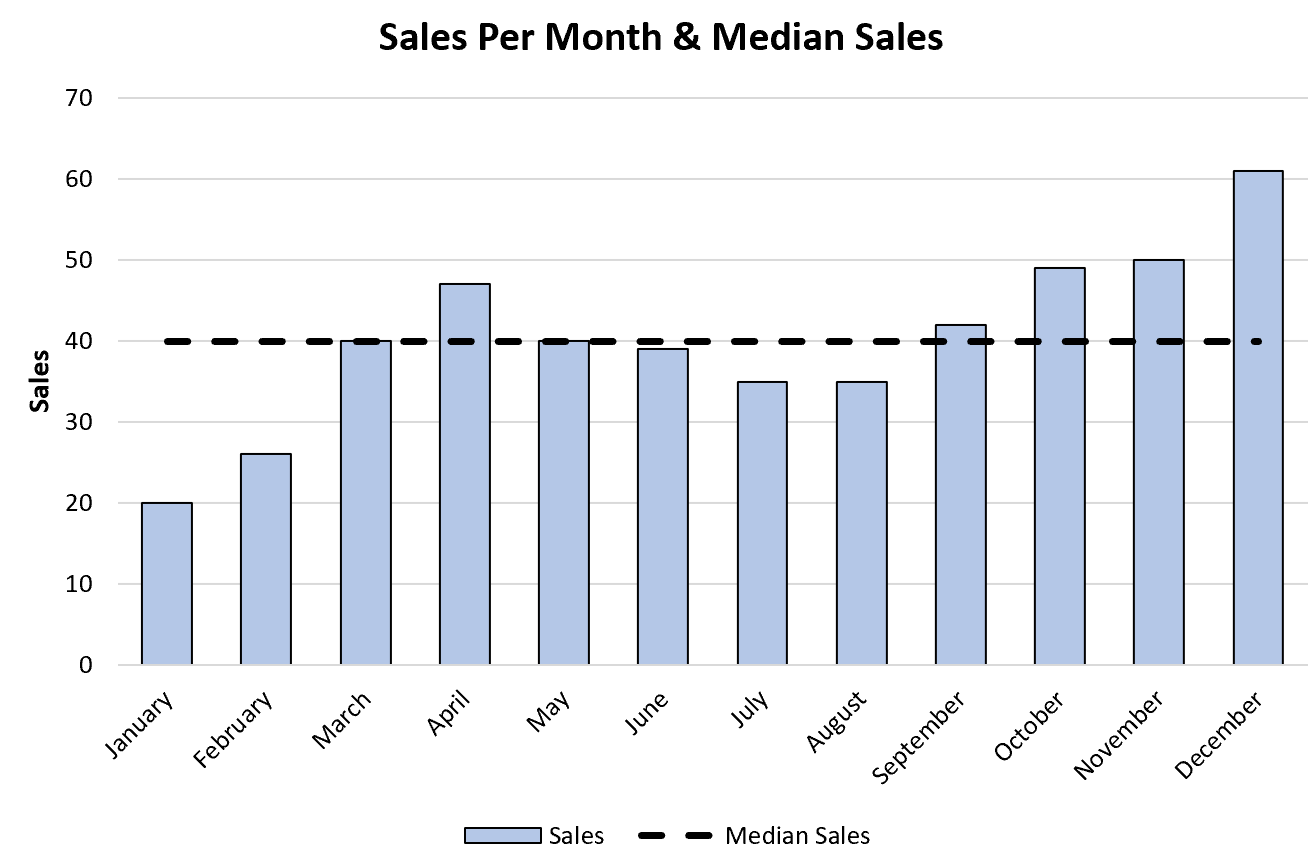
Have you ever looked at a graph and wondered what the median represents? The median is a crucial piece of information that can give you a better understanding of the data at a glance.
When you see the term “median in a graph,” it refers to the middle value of a dataset when it is arranged in numerical order. Unlike the mean, which is the average value, the median is not affected by extreme values, making it a more robust measure of central tendency.
median in a graph
Understanding the Median in a Graph
For example, if you have a dataset of 1, 2, 3, 4, and 100, the median would be 3. Even though the mean would be significantly higher due to the outlier of 100, the median accurately represents the middle value of the dataset.
Calculating the median in a graph is simple. Just arrange the data points in numerical order and find the middle value. If there is an even number of data points, take the average of the two middle values to find the median.
By understanding the median in a graph, you can gain insights into the distribution of data and identify any potential outliers that may skew the results. It is a valuable tool for analyzing data in various fields, from statistics to finance and beyond.
Next time you come across a graph, take a moment to look for the median value and consider what it tells you about the dataset. It’s a small but powerful piece of information that can enhance your data interpretation skills.
Mean Median And Mode KSJ Handbook
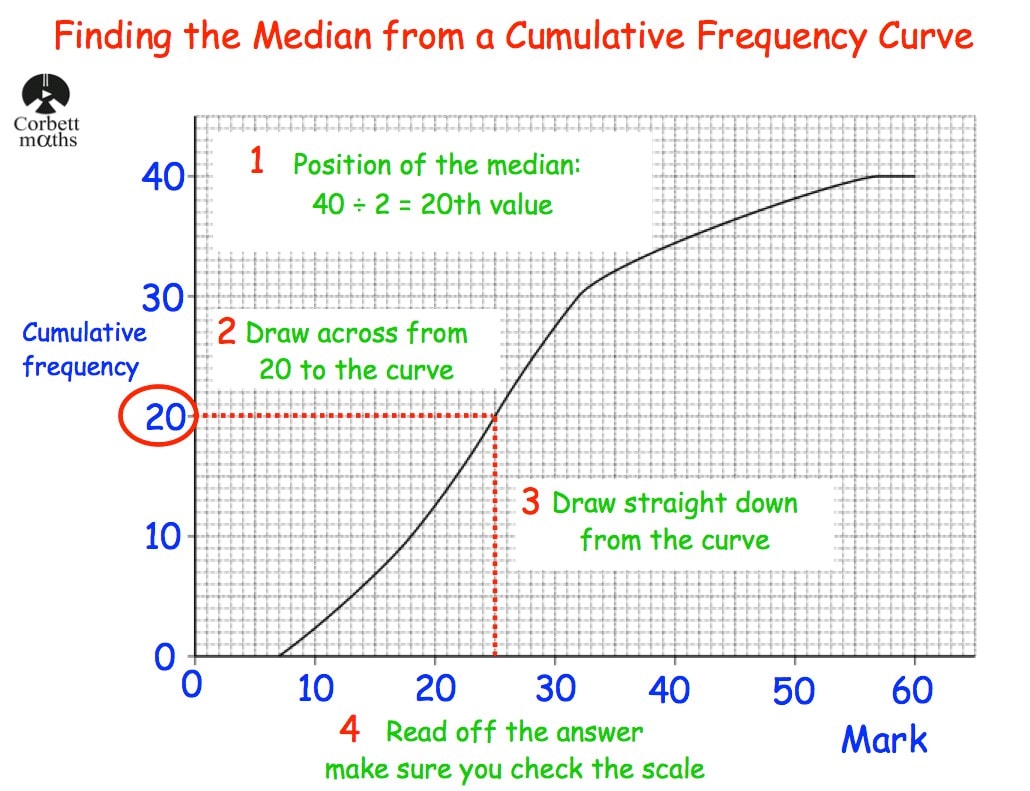
Median From A Frequency Distribution MATH MINDS ACADEMY
Central Tendency Understanding The Mean Median Mode
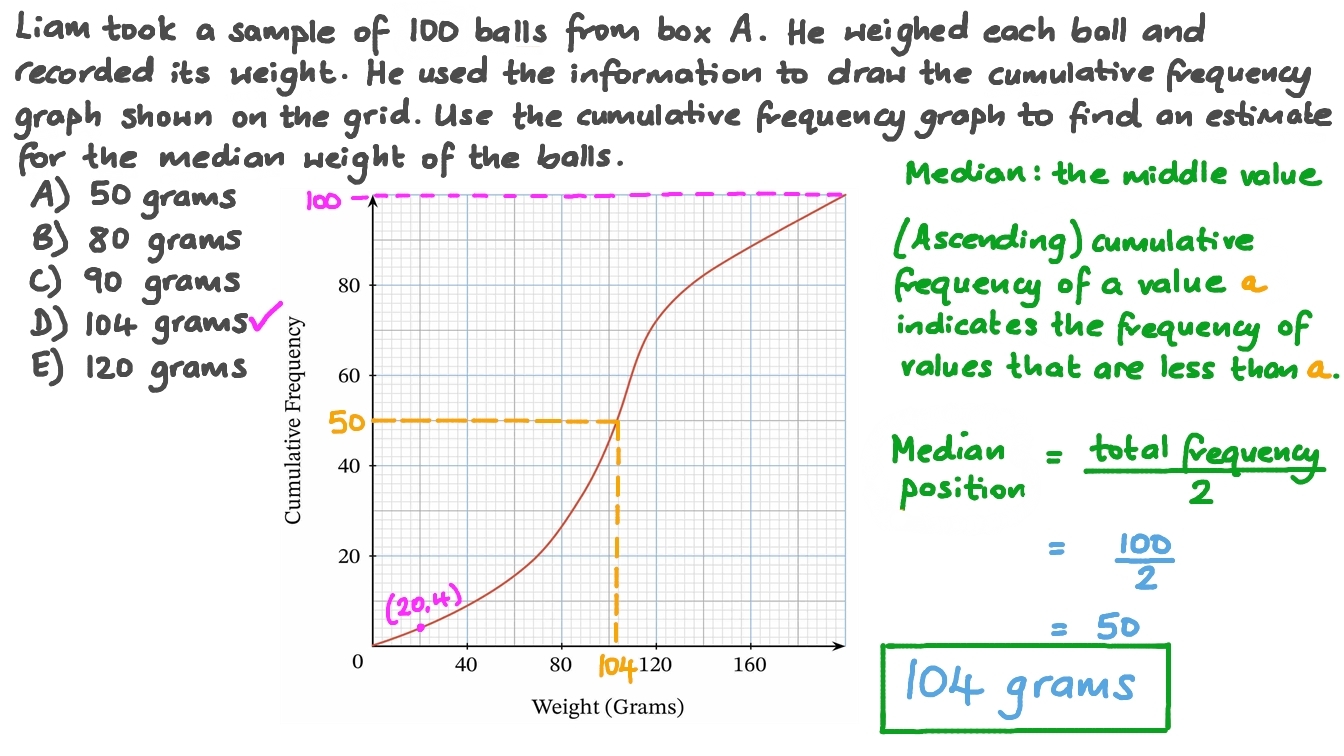
Question Video Estimating The Median From A Cumulative Frequency Graph Nagwa
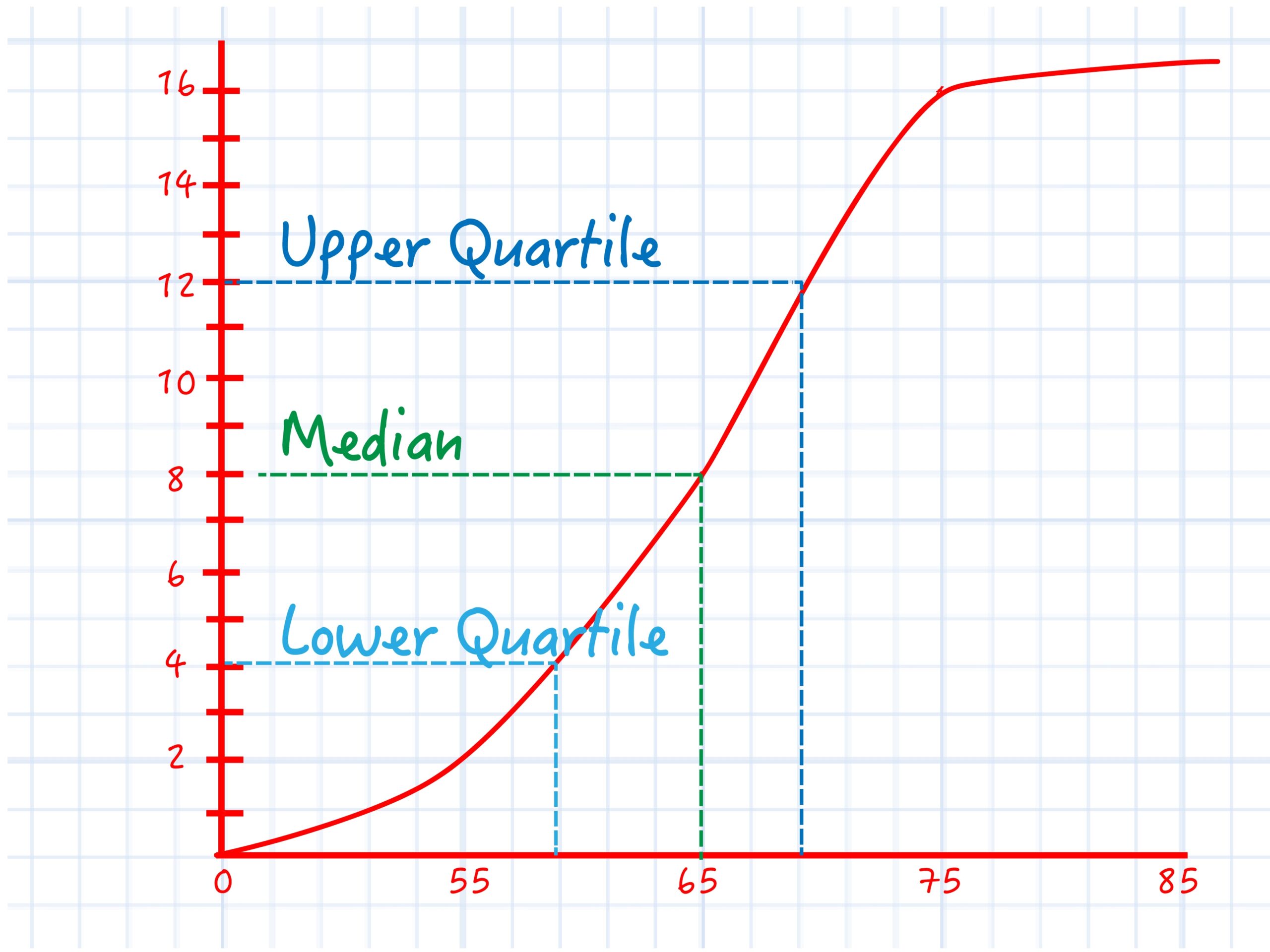
How To Calculate Cumulative Frequency 11 Steps with Pictures