Have you ever wondered about the geometry of shapes inside a circle? One interesting concept to explore is a quadrilateral inscribed in a circle. This unique shape has some fascinating properties that make it worth learning about.
When a quadrilateral is inscribed in a circle, it means that all four vertices of the quadrilateral lie on the circumference of the circle. This creates a beautiful relationship between the angles and sides of the quadrilateral, leading to some intriguing mathematical implications.
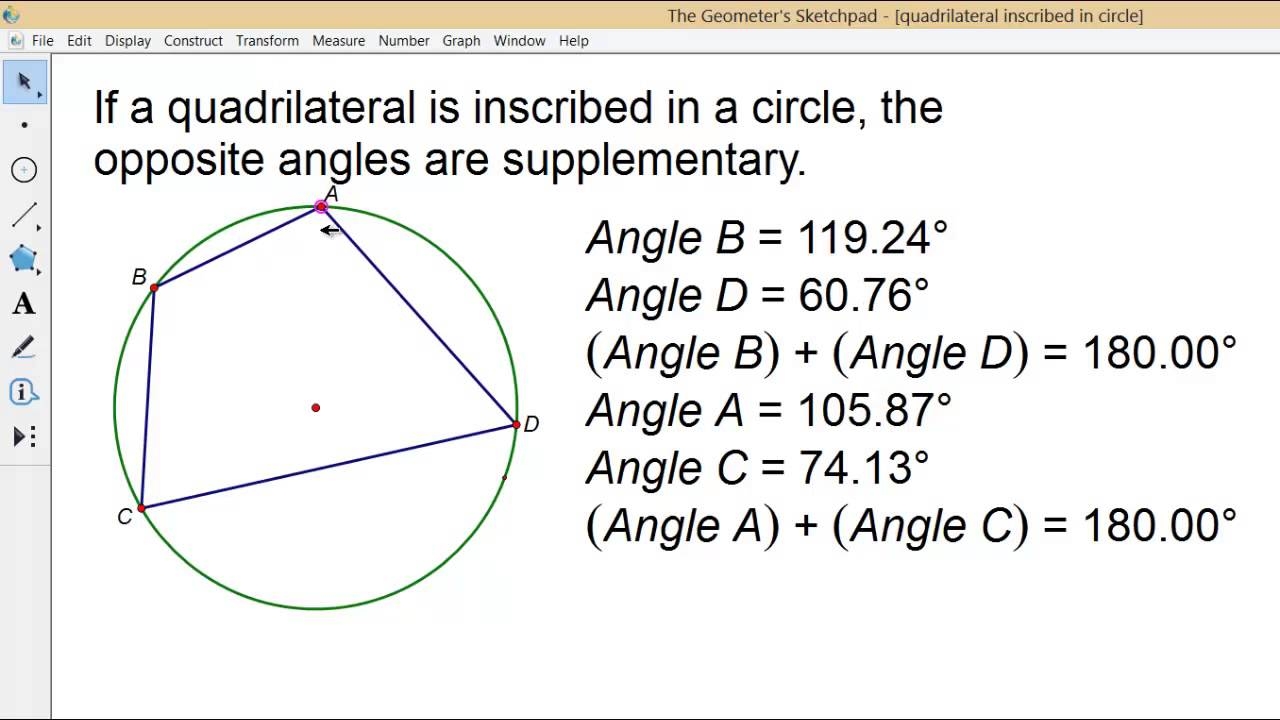
quadrilateral in a circle
The Beauty of a Quadrilateral in a Circle
One key property of a quadrilateral inscribed in a circle is that opposite angles are supplementary. This means that the sum of two opposite angles adds up to 180 degrees. This relationship can be useful when solving geometry problems involving quadrilaterals in circles.
Additionally, the diagonals of a quadrilateral inscribed in a circle are perpendicular to each other. This perpendicularity creates right angles at the intersection point of the diagonals, adding another layer of complexity to the geometry of the shape.
Furthermore, the sum of the measures of the angles of a quadrilateral inscribed in a circle is always 360 degrees. This property can be leveraged to find missing angles or solve for unknown variables in geometric calculations involving quadrilaterals in circles.
Exploring the intricacies of quadrilaterals inscribed in circles can be both challenging and rewarding. By understanding the unique properties of these shapes, you can enhance your geometric knowledge and problem-solving skills. So, next time you encounter a quadrilateral in a circle, remember to consider the fascinating relationships it entails.
Tangential Quadrilateral Wikipedia
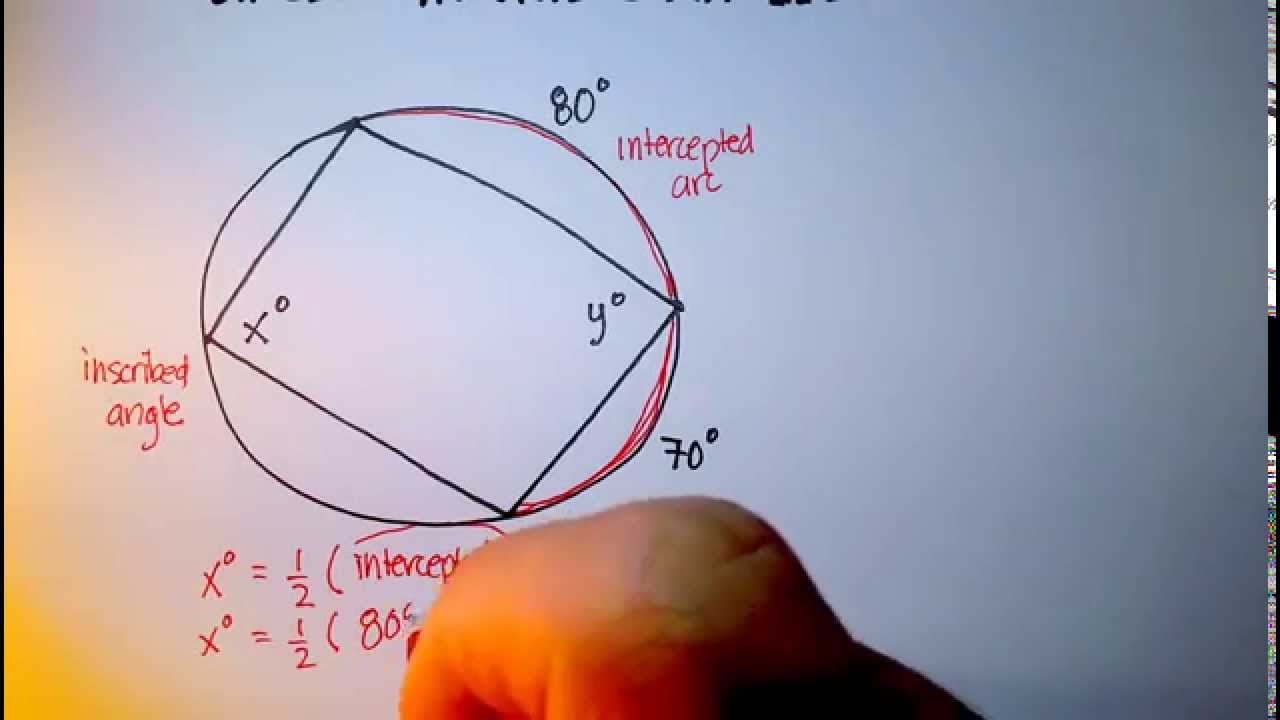
Circles Inscribed Angles Quadrilateral YouTube
Pt 3 Reattempting Circle Theorems Conception Of The Good
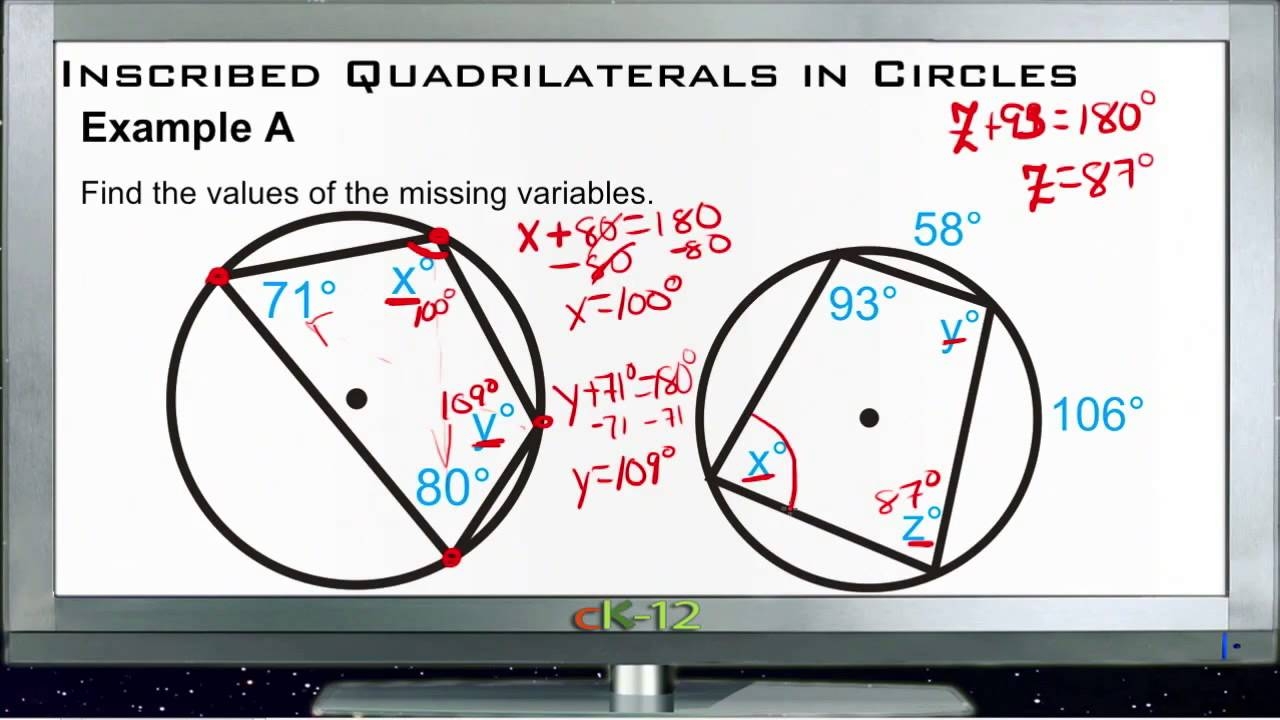
Inscribed Quadrilaterals In Circles Examples Basic Geometry Concepts YouTube
Cyclic Quadrilateral Wikipedia